נניח שאנחנו צופים במשחק כדורגל. המשחק בדיוק התחיל והתוצאה היא 0-0.
מה הסיכוי שהמשחק יסתיים עם 3 גולים?
נסו לנחש מספר שנראה לכם הגיוני ותכף נראה אם צדקתם.
מה הסיכוי שהמשחק יסתיים עם 50 גולים?
מאד נמוך, נכון?
איך קבענו את זה? כי אנחנו יודעים שבמשחקי כדורגל לא מגיעים ל-50 גולים.
ומה הסיכוי שמשחק כַּדּוּרְיָד יסתיים עם 50 גולים?
למי שלא מכיר, משחקי כדוריד מסתיימים לרוב בטווח של 40-70 גולים .
לכן, הפעם יש סיכוי לא רע ל-50 גולים במשחק.
אנחנו רואים, שאם נרצה לחזות מה הסיכוי של תוצאה מסויימת, חשוב שיהיה לנו מידע מוקדם על הממוצע.
התפלגות פואסון היא בדיוק מודל שכזה, המשמש לחזות את מספר האירועים שיתרחשו בפרק זמן מסויים (למשל משחק כדורגל), אם ידוע לנו הממוצע.
הממוצע נקרא גם: קצב ההתרחשות.
במילים פשוטות –
זו נוסחה , שאם נציב בה את הממוצע λ הידוע לנו, נוכל לגלות מה הסיכוי ש-k יקרה :
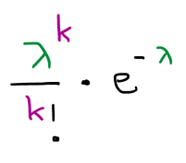
( λ זו האות לַמְדַא ביוונית. נהוג לכתוב את הנוסחה עם האות הזו דווקא, אבל אפשר היה לבחור בכל אות אחרת. e הוא מספר ששווה בערך ל-2.7 . ואם אתם שואלים איך הגיעו לנוסחה הזו, זו שאלה מצויינת, שנענה עליה בהמשך)
נראה דוגמה :
לפי הנתונים המתפרסמים באינטרנט, בכל משחק במונדיאל, גביע העולם בכדורגל, יש 2.5 גולים בממוצע, כלומר 2.5=λ .
עכשיו כשיש לנו את הממוצע, אנחנו רוצים לחשב מה הסיכוי שהמשחק הבא במונדיאל יגמר ללא גולים , כלומר k=0.
נציב 2.5=λ ו – k=0 בנוסחת פואסון ונחשב במחשבון:
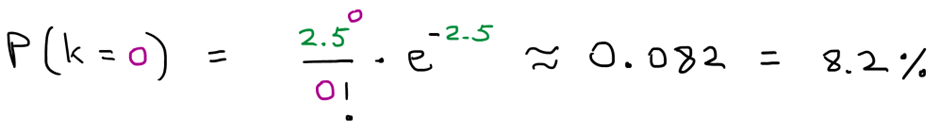
כלומר, אם הממוצע הוא 2.5 אז הסיכוי שהמשחק יסתיים עם 0 גולים הוא 8.2% .
מה הסיכוי שמשחק יגמר עם שני גולים ? נציב 2.5=λ ו – k=2 :
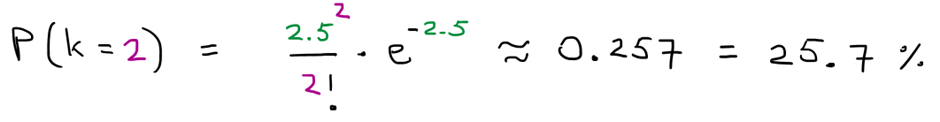
אם נמשיך ונחשב ככה עבור עוד ערכי k נקבל את הטבלה הבאה:
| מס' הגולים במשחק – k | הסיכוי – P(k) |
| 0 | 8.2% |
| 1 | 20.5% |
| 2 | 25.7% |
| 3 | 21.3% |
| 4 | 13.3% |
| 5 | 6.7% |
| 6 | 2.8% |
ניתן לראות מהטבלה שהסיכוי הגבוה ביותר הוא ל-2 גולים (k=2) – 25.7%
לאחר מכן, במקום השני, הסיכוי ל-3 גולים (k=3) – 21.3%
קצת מוזר. היינו מצפים, אולי, שתהיה סימטריה בין השניים –
כלומר שהסיכוי ל-2 גולים יהיה זהה לסיכוי ל-3 גולים, כי הקצב הממוצע 2.5=λ הוא בדיוק באמצע .
אבל זה לא קורה.
התפלגות פואסון היא מוטה (skewed) ולא סימטרית.
דוגמה נוספת :
מייקל ג'ורדן קולע סל בממוצע כל 4 דקות . מה הסיכוי שלא נראה אף סל שלו במשך רבע שלם?
(רבע ב-NBA הוא 12 דקות)
מכיוון שהשאלה מתייחסת לפרק זמן של 12 דקות, נחשב את הממוצע λ ל-12 דקות.
אם הוא קולע 1 סלים כל 4 דקות,
אז הוא קולע 3 סלים כל 12 דקות
(כפלנו פי 3) .
אם כך λ=3 (ל-12 דקות).
נציב ונקבל שהסיכוי ל-0 סלים ב-12 דקות הוא 4.9% .
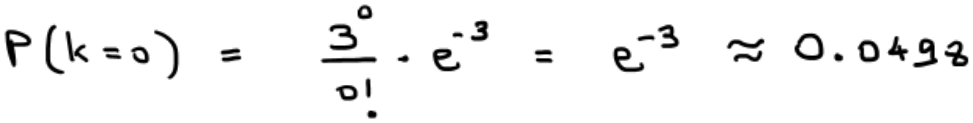
שימו לב שבדוגמה הראשונה הממוצע λ הוא למשחק שלם (זו יחידת הזמן), בעוד שבדוגמה השניה הממוצע λ הוא ל-12 דקות (זו יחידת הזמן).
תמיד נבחר את יחידת הזמן לפי מה שנרצה לחשב.
אפשר לומר שהמודל של פואסון יתאים לנו במקרים הבאים:
- האירועים לא תלויים אחד בשני (אם הובקע גול זה לא משפיע על הסיכוי לגול נוסף)
- קצב האירועים הממוצע λ הוא קבוע ולא משתנה כתלות בזמן
- שני אירועים לא יכולים לקרות בו זמנית (אין שני גולים באותה שניה)
אפשר לטעון ולומר שלא כל התנאים מתקיימים ב-100% . למשל, לאחר שמובקע גול, המאמן עלול לבצע חילוף ולשנות הרכב, מה שמעלה או מוריד את הסיכוי לגול נוסף.
אתם צודקים. המודל הזה, כמו במקרים רבים בהסתברות ובפיזיקה, הוא רק קירוב למציאות –
All models are wrong, but some are useful 😊
זמן המתנה
נסעתם למצפה רמון לראות מטר מטאורים. חבר שהיה שם אתמול אמר לכם שהיה שם סך הכל 2 שעות וראה 4 מטאורים, כלומר יצא בממוצע שכל 30 דקות היה מטאור.
(בזמן מטר גדול אפשר לראות הרבה הרבה יותר מזה, אבל נזרום עם הדוגמה…).
אז הגעתם. כיביתם אורות, פרשתם שמיכה.
כמה זמן בממוצע תחכו עד שתראו לראשונה מטאור?
כששאלתי פעם חבר מה לדעתו התשובה הוא ענה ככה:
יתכן שהופיע מטאור שניה לפני שהגעתם, לכן תחכו בממוצע 30 דקות. אבל יתכן שבדיוק אחרי שהגעתם יופיע מטאור ולכן חיכיתם 0 דקות. לכן הממוצע הוא 15 דקות.

נשמע הגיוני, אבל האם זה באמת נכון?
כדי לענות, בואו נתחיל מלבדוק קודם שאלה אחרת –
מה הסיכוי שנחכה יותר מ-15 דקות, מרגע שהגענו?
ראינו שנוסחת פואסון משמשת כדי לחשב את הסיכוי שאירוע עתידי כלשהו יקרה (למשל מה הסיכוי שיהיו סה"כ 2 גולים במשחק, אם ידוע שהממוצע הוא 2.5 גולים).
האם אפשר להשתמש בנוסחה הזו גם כדי לחשב זמן המתנה?
נבדוק.
אם יש 1 מטאור כל 30 דקות, אפשר לומר שיש 1/30 מטאור כל 1 דקות (חילקתי ב-30).
כלומר 1/30 = λ (מטאורים לדקה).
מה הסיכוי שבדקה הקרובה לא יהיה אף מטאור?
על זה נוכל לענות בקלות. נציב k=0 (עבור 0 מטאורים) בנוסחת פואסון :
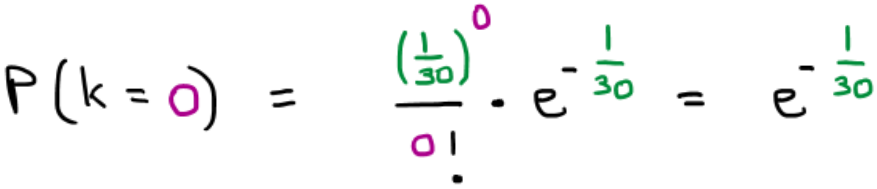
שימו לב שיחידת הזמן כאן היא דקה. לעומת זאת, יחידת הזמן בדוגמת המונדיאל היתה משחק שלם. יחידת הזמן בדוגמה עם מייקל ג'ורדן היתה 12 דקות.
מה הסיכוי שבשתי הדקות הקרובות לא יהיה מטאור? זה הסיכוי שבדקה הקרובה לא יהיה אף מטאור וגם בדקה שאחריה לא יהיה. מכיוון שהמאורעות לא תלויים אפשר לכפול ביניהם:

מה הסיכוי שב-15 הדקות הקרובות לא יהיה מטאור? נכפול את הביטוי 15 פעמים ונקבל:

שימו לב, הסיכוי שבמשך 15 דקות לא יהיו מטאורים הוא בדיוק הסיכוי שנמתין יותר מ-15 דקות.
לכן, הסיכוי שזמן ההמתנה T יהיה גדול מ-15 דקות הוא בדיוק מה שחישבנו :

כלומר, בעזרת נוסחת פואסון הצלחנו לחשב מה הסיכוי שזמן ההמתנה (עד למטאור הבא) יהיה גדול מ-15 דקות – קיבלנו שהסיכוי שזה יקרה הוא 60.65%.
ובאופן כללי, הסיכוי שזמן ההמתנה יהיה גדול מ-t כלשהו :
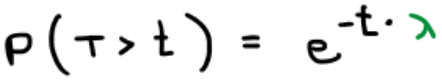
לכן הסיכוי שזמן ההמתנה יהיה קטן-שווה מ-t כלשהו : (הסתברות משלימה – אחת פחות מה שקיבלנו)
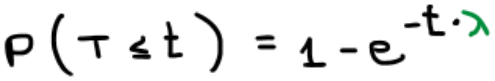
כלומר, הסיכוי שזמן ההמתנה למטאור הבא יהיה 15 דקות או פחות מזה, הוא :
60.65% – 100% = 39.35%
מה שקיבלנו היא פונקציה שמתארת התפלגות מעריכית .
ההתפלגות המעריכית בסך הכל מתארת זמן המתנה (בין אירוע לאירוע) בתהליך פואסון. למשל: כמה זמן נמתין בין שני מטאורים, או בין שני גולים במשחק, או בין שני אוטובוסים וכו'
אם מספר האירועים ליחידת זמן מתואר ע"י התפלגות פואסון, אז פרק הזמן בין האירועים מתואר ע"י ההתפלגות המעריכית. שתיהן קשורות זו לזו.
נסכם:
| הסיכוי שזמן ההמתנה יהיה גדול מ-t כלשהו : | 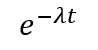 |
| הסיכוי שזמן ההמתנה יהיה קטן-שווה ל-t כלשהו : | 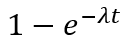 |
ותרגיל קטן לסיום:
מה הסיכוי שנחכה בין 10 ל-20 דקות עד המטאור הבא?
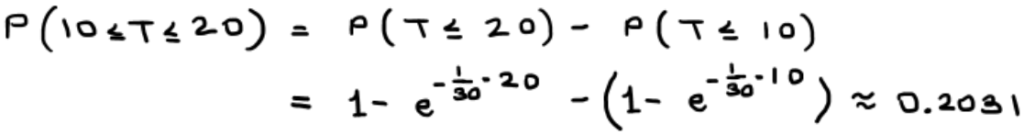
עכשיו כשאנחנו יודעים לחשב מה הסיכוי שנחכה יותר מ-15 דקות (או כל מספר אחר במקום 15 כמובן) – נראה מקרה נוסף שאולי יצליח להפתיע.
חוסר זכרון
נניח שכבר חיכינו 30 דקות ולא ראינו מטאור. מה הסיכוי שזמן ההמתנה , לאחר שכבר חיכינו 30 דקות, יהיה גדול מ-15 דקות ?
כדי לענות על זה נחשב –
מה הסיכוי שבדקה הקרובה לא יהיה אף מטאור?
נציב k=0 (עבור 0 מטאורים) בנוסחת פואסון :
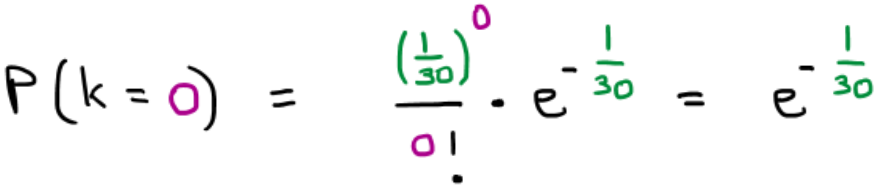
נרצה שגם בדקה השניה לא יהיה אף מטאור, ובדקה השלישית, ובזו שאחריה – ככה למשך 15 פעמים:
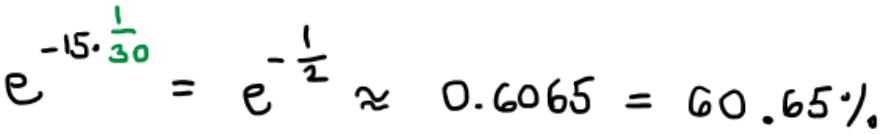
רגע רגע רגע… זה בדיוק אותו חישוב ואותה תוצאה כמו בפעם הקודמת.
מה קורה פה?
מצד אחד – יש סיכוי של 60.65% שזמן ההמתנה, מרגע שהגענו, יהיה יותר מ-15 דקות (את זה חישבנו למעלה).
מצד שני – אם כבר חיכינו 30 דקות אז הסיכוי שנחכה יותר מ-15 דקות הוא אותו דבר בדיוק – 60.65% (את זה חישבנו ממש עכשיו).
זה מאד נוגד את ההיגיון, לא?
נדמה לנו שאם חיכינו זמן רב אז הקטנו את הסיכוי שנחכה שוב הרבה זמן, אבל זה לא עובד ככה, עיניכם הרואות! החישוב הוא אותו חישוב והתוצאה אותה תוצאה.
התכונה המעניינת הזו נקראת חוסר זכרון . אנחנו אומרים שזמן ההמתנה הוא חסר זכרון.
כלומר – הסיכוי להמתין יותר מ-t דקות (למטאור הבא או לאוטובוס הבא) לאחר שחיכינו כבר זמן כלשהו (קצר או ארוך), זהה לסיכוי כאילו לא חיכינו רגע אחד.
עדיין נשמע לא הגיוני? אתן דוגמה שתעזור לעכל את זה.

מטילים קוביה רגילה. מה הסיכוי שתצא הספרה 5 ?
הסיכוי הוא כמובן 1/6 .
בממוצע ולאורך זמן, אם נטיל קוביה הרבה פעמים, שישית מהפעמים נקבל את הספרה 5.
עכשיו נניח שזרקתם את הקוביה 20 פעמים ולא יצא 5 אפילו פעם אחת. מה הסיכוי שבהטלה הבאה תצא הספרה 5?
הסיכוי הוא עדיין 1/6 , כי יש שש פאות לקוביה , ורק על פאה אחת כתוב 5.
עצם זה ש"חיכינו" הרבה זמן לספרה 5 והיא טרם הופיעה, לא גורם לה "להופיע מהר יותר".
כלומר, המידע שבעשרים ההטלות הקודמות לא הופיעה הספרה 5 לא שינה דבר – הסיכוי שתהיה "הצלחה" נשאר זהה.
אז חוסר זכרון מופיע גם במקרה זה של הטלת קוביה.
* * * * *
אם כך ראינו שההתפלגות המעריכית עוסקת בזמן ההמתנה (בתהליך פואסון) בין שני אירועים עוקבים.
וכן שהסיכוי שנמתין יותר מ-15 דקות הוא זהה, לא משנה מהיכן הוא נמדד – מהרגע שהגענו, מרגע שסיימנו 30 דקות המתנה, או מרגע הופעת המטאור הקודם.
בפוסט הבא אוכיח מתמטית את תכונת חוסר הזכרון של ההתפלגות המעריכית וגם נענה סוף סוף על השאלה שהתחילה את הכל –
מהו זמן ההמתנה הממוצע ?